8.1 트리의 개념
스택, 큐, 리스트는 모두 자료들이 일렬로 나열된 형태인 선형 자료구조linear data structure이다. 하지만 자료들이 계층 구조를 가지고 있다면? 컴퓨터 폴더 구조나 가계도, 조직도 등의 자료를 표현하고 싶을 땐 선형 구조로는 충분하지 않다. 이렇게 계층적 구조hierarchical structure를 표현하는 데 이용되는 자료구조가 트리tree이다.
트리의 용어

트리의 구성 요소에 해당하는 A, B, C, ..., K, L을 노드node라고 한다. 트리는 한 개 이상의 노드로 이루어진 유한 집합이다. 계층 구조에서 가장 위에 있는 노드를 루트 노드root node라고 한다. 위의 그림 8.1에서의 루트 노드는 A이다. 루트를 뺀 나머지 노드들은 서브트리subtree라고 부른다. 전체 노드 집합 {A, B, C, D, E, F, G, H, I, J, K, L} 중 루트 노드인 A를 제외한 나머지 노드들은 {B, E, F, J, K}, {C}, {D, G, H, I, L}의 3개의 집합으로 나눌 수 있다. 이 3개의 집합이 A의 서브트리이다. 서브트리 역시 서브트리의 노드와 그 서브트리로 나눌 수 있다. A의 서브트리인 {D, G, H, I, L}의 루트는 D가 되고, 나머지 노들은 다시 3개의 서브트리, {G, L}, {H}, {I}로 나누어진다.
트리에서 루트와 서브트리는 선으로 연결된다. 이 선을 엣지edge라고 부르며 노드 들 간에는 부모, 형제, 조상, 자손 관계가 존재한다. 이들은 이름이 가진 의미와 동일하다. 그림 8.1 상에서 A는 B의 부모 노드parent node이며 반대로 B는 A의 자식 노드children node이다. 노드 B, C, D는 형제 관계sibling이다. 조상 노드ancestor node는 루트 노드에서 임의의 노드까지의 경로를 이루는 모든 노드를 말하며 자손 노드descendent node는 임의의 노드 하위에 연결된 모든 노드를 말한다. 즉, 어떤 노드의 서브트리에 속하는 모든 노드들은 그 노드의 자손 노드이다. 자손 노드가 없는 노드는 단말 노드terminal/leaf node라고 한다. 그림 8.1에서는 E, J, K, L, H, I가 단말 노드이며 반대로 자식 노드가 있으면 비단말 노드nonterminal node라고 한다.
노드의 차수degree는 어떤 노드가 가진 자식 노드의 개수라고 한다. 그림 8.1에서 루트 노드는 3개의 자식 노드를 가지므로 차수가 3이다. 따라서 단말 노드는 차수가 0이다. 트리의 차수는 트리가 가진 노드의 차수 중 가장 큰 차수이다. 위의 그림 8.1에서는 노드 A와 D의 차수인 3이 가장 크므로 위 트리의 차수는 3이다. 레벨level은 트리의 각 층에 매긴 번호로, 루트 노드부터 시작하여 한 층씩 내려갈수록 1을 더한다. 따라서 루트 노드의 레벨은 항상 1이다. 위 그림 8.1에서 G의 레벨이다. 트리의 높이height는 트리가 가진 최대 레벨을 뜻한다. 위의 트리는 최대 레벨 4이므로 높이는 4이다.
트리의 표현
트리를 표현하는 방법에는 여러 가지가 있지만 가장 일반적으로는 노드 구조를 이용한다. 각 노드는 데이터를 저장하는 데이터 필드와 자식 노드를 가리키는 링크 필드를 가진다. 이때 링크 필드의 개수는 자식 노드의 개수, 즉 해당 노드의 차수가 되어야 한다. 하지만 일반 트리에서 각 노드들은 임의의 개수의 자식 노드를 가지기 때문에 링크 필드의 개수를 일정하게 관리할 수 없다. 그래서 프로그램의 효율성과 나은 관리를 위해 두 개의 자식 노드를 사용하는 이진트리binary tree를 많이 사용한다. 이진트리는 자식 노드의 개수가 항상 2개 이하인 트리를 말한다.
8.2 이진트리 소개
이진트리란?
이진트리는 모든 노드가 2개의 서브트리를 갖는 트리로, 이때 서브트리는 공집할일 수도 있다. 따라서 모든 노드의 차수는 2 이하가 되어 최대 2개까지의 자식 노드(없거나, 1개거나, 2개거나)를 가질 수 있다. 이진트리의 서브트리는 순서가 존재하는데, 항상 왼쪽 서브트리와 오른쪽 서브트리는 구분되어야 한다.
이진트리의 정의는 다음과 같다.
(1) 공집합이거나
(2) 루트와 왼쪽 서브트리, 오른쪽 서브트리로 구성된 노드들의 유한 집합. 이진트리의 서브트리들은 모두 이진트리이다.

그림 8.2의 트리가 이진트리인지 검증하여 보자.
D, H, F, I의 자식 노드는 공집합이다. 공집합도 이진트리이다. E와 G는 각각 H, I과 공집합을 자식 노드로 가지므로 E와 F를 루트로 하는 서브트리는 이진트리이다. B와 C는 이하의 이진트리를 서브트리로 가진다. 전체 트리를 살펴보면 루트 노드 A와 B, C를 각각 루트로 갖는 서브트리를 가지는 이진트리이다.
따라서 이진트리이다.
이진트리의 종류

이진트리는 형태에 따라 포화 이진트리full binary tree, 완전 이진트리complete binary tree, 기타 이진트리로 분류할 수 있다.
포화 이진트리는 트리 각 레벨에 노드가 꽉 찬 이진트리를 말한다. 즉 높이 k인 포화 이진트리는 2^(k-1) 개의 노드를 가진다. 포화 이진트리에서는 각 노드에 번호를 붙일 수 있는데 레벨 단위로, 왼쪽에서 오른쪽으로 번호를 붙이고 이 번호는 항상 일정하다. 예를 들어, 루트 노드의 오른쪽 자식 노드는 항상 3이다.
완전 이진트리는 높이가 k인 트리에서 레벨 1부터 k-1는 노드가 모두 채워져 있고, 마지막 레벨 k에서는 왼쪽부터 오른쪽으로 노드가 순서대로 채워진 이진트리를 말한다. 마지막 레벨에서는 노드가 꽉 차있지 않아도 되지만 중간에 빈 곳이 있으면 안 된다.
따라서 포화 이진트리는 완전 이진트리에 속하며 그 역은 성립하지 않는다. 힙heap이 완전 이진트리의 대표적인 예시라고 할 수 있다.
이진트리의 성질
n개의 노드를 가진 트리는 (n-1) 개의 엣지를 가진다.
높이가 h인 이진트리의 노드는 h개 이상, 2^(k-1) 개 이하이다.
n개의 노드를 가지는 이진트리의 높이는 log2의 (n+1) 이상 n 이하이다.
이진트리의 추상 자료형
이진트리를 추상 자료형으로 정의해보자.
객체: 노드와 엣지의 집합. 노드는 공집합이거나 공집합이 아닌 경우 루트노드와 왼쪽 서브트리, 오른쪽 서브트리로 구성되며 모든 서브트리도 이진트리여야 한다.
연산:
create(): 이진트리를 생성한다
isEmpty(): 이진트리가 공백 상태인지 확인한다
getRoot(): 이진트리의 루트 노드를 반환한다
getCount(): 이진트리의 노드 수를 반환한다
getHeight(): 이진트리의 높이를 반환한다
insertNode(n): 이진트리에 노드 n을 삽입한다
deleteNode(n): 이진트리에서 노드 n을 삭제한다
display(): 이진트리의 내용을 화면에 출력한다
8.3 이진트리의 표현
배열을 이용한 표현 방법과 포인터를 이용하는 연결된 표현 방법(링크 표현법)이 있다.
배열 표현법

이 방법은 저장하고하 하는 이진트리가 완전 이진트리라고 가정하고 그 높이가 k이면 (2^k-1)개의 공간을 연속적으로 할당하고 완전 이진트리의 번호대로 노드의 정보를 배열에 저장한다. 이때 인덱스 0은 사용하지 않는다. 이 방법은 주로 포화 이진트리, 완전 이진트리에서 많이 사용되지만 높이가 k인 트리가 가질 수 있는 최대 노드 개수만큼 공간을 할당하므로 일반 이진트리도 저장할 수 있다. 하지만 메모리 낭비가 심할 수 있다.
배열 표현법에서 부모와 자식 인덱스의 관계를 살펴보자. 배열 표현법에서는 인덱스만 알면 어떤 노드의 부모나 자식을 쉽게 알 수 있다. 부모와 자식 인덱스 사이에는 다음과 같은 공식이 성립한다.
노드 i의 부모 인덱스 = i/2
노드 i의 왼쪽 자식 노드 인덱스 = 2i
노드 i의 오른쪽 자식 노드 인덱스 = 2i + 1
링크 표현법

링크 표현법은 연결 리스트를 이용한 선형 자료구조의 표현 방식과 유사하다. 트리의 노드들은 메모리 공간 상 흩어져 있고 한 노드는 데이터 필드와 링크 필드를 갖는다. 링크 표현법에서의 이진트리 노드는 이중 연결 리스트의 노드에서와 같이 2개의 포인터 변수를 가지며 각각 왼쪽 자식 노드와 오른쪽 자식 노드를 가리킨다.
그림 8.4에서의 트리를 링크 표현법으로 다시 그려보면 다음과 같다.

8.4 링크 표현법을 이용한 이진트리
다음은 이진트리를 위한 노드 클래스를 구현한 BinaryNode.h이다.
//BinaryNode.h
#pragma once
#include <stdio.h>
class BinaryNode
{
protected:
int data;
BinaryNode *left;
BinaryNode *right;
public:
BinaryNode( int val=0, BinaryNode *l=NULL, BinaryNode *r=NULL)
: data(val), left(l), right(r) { }
~BinaryNode() { }
void setData ( int val ) { data = val; }
void setLeft (BinaryNode *l) { left = l; }
void setRight(BinaryNode *r) { right = r; }
int getData () { return data; }
BinaryNode* getLeft () { return left; }
BinaryNode* getRight() { return right; }
bool isLeaf() { return left==NULL && right==NULL; }
};
이진트리의 노드를 정의하는 헤더 파일에는, BinaryNode 클래스를 통해 이진트리를 위한 노드 클래스를 작성한다. 멤버 변수로는 트리에 저장할 데이터인 int형 data 변수, 왼쪽 자식 노드를 가리키는 포인터 변수인 left와 오른쪽 자식 노드를 가리키는 포인터 변수인 right가 있다. 생성자는 디폴트 매개변수를 사용해서 데이터 멤버를 초기화하였다. 데이터를 설정하는 setData(), setLeft(), setRight() 함수는 각각 트리에 저장할 데이터, 왼쪽 자식 노드를 가리킬 포인터, 오른쪽 자식 노드를 가리킨 포인터를 설정하고 getData(), getLeft(), getRight()는 각각 이들을 반환하는 함수이다. isLeaf()는 bool 타입 함수로, 왼쪽과 오른쪽의 자식 노드가 모두 NULL값일 때 1을 반환하여 현재 노드가 단말 노드인지 검사한다.
이진트리 클래스의 구현은 순회와 추가 연산 후에 다시 다루도록 하자.
8.5 이진트리의 순회
트리를 순회traversal한다는 것은 트리에 속하는 모든 노드를 한 번씩 방문하여 노드가 가진 데이터를 목적에 맞게 처리하는 것을 의미한다. 우리가 트리를 사용하는 목적은 틔 노드에 자료를 저장하고 필요에 따라 이를 처리하기 위함이므로 트리의 노드들을 모두, 순차적으로 방문하는 것은 가장 기본적인 연산이다. 선형 자료구조에서는 자료가 순차적으로 저장되어 있으므로 순회 방법이 하나뿐이지만 계층 구조를 갖는 트리는 여러 가지 순회 방법이 있다.
이진트리 순회 방법
이진트리를 순회하는 표준적인 방법에는 전위, 중위, 후위의 3가지 방법이 있다. 이는 루트와 왼쪽, 오른쪽의 서브트리를 어떤 순서로 각각 방문하느냐에 따라 구분된다. 루트를 방문하는 것을 V, 왼쪽 서브트리의 방문을 L, 오른쪽 서브트리 방문을 R이라고 한다면 3가지의 순회 방법을 다음과 같이 표현할 수 있다.
전위 순회preorder traversal: VLR
중위 순회inorder traversal: LVR
후위 순회postorder traversal: LRV
조금 더 간단히 화살표로 표현하자면 다음과 같다. 각 삼각형의 꼭지점은 위, 왼쪽, 오른쪽 차례대로 루트 노드, 왼쪽 서브트리와 오른쪽 서브트리를 방문하는 것을 뜻한다.

이진트리는 전체 트리와 서브트리가 구조는 완전히 동일하고 그 크기만 달라지므로 전체 트리 순회에 사용된 알고리즘을 똑같이 서브트리에 적용할 수 있다.
전위 순회부터 살펴보자. 전위 순회는 루트를 먼저 방문한 후 왼쪽 서브트리를 방문하고, 오른쪽 서브트리를 마지막으로 방문한다. 전위 순회에서 루트 노드의 방문을 마쳤다고 가정하면 다음은 왼쪽 서브트리를 방문할 차례이다. 그러면 왼쪽 서브트리의 어떤 노드를 먼저 방문해야 할까? 왼쪽 서브트리도 하나의 이진트리이므로 전체트리와 같은 방식으로 서브트리부터 방문한다. 즉 모든 서브트리에 대하여 같은 알고리즘을 반복한다.
다음은 전위 순회를 구현한 것이다.
void preorder(BinaryNode *node) {
if( node != NULL ) {
printf( " [%c] ", node->getData());
if( node->getLeft() != NULL ) preorder(node->getLeft());
if( node->getRight()!= NULL ) preorder(node->getRight());
}
}node 포인터를 사용하여 NULL이 아닐 때 루트 노드를 출력하고 왼쪽 서브 트리부터 방문한다. 왼쪽 자식 노드가 NULL이 아닐 때 방문하고, 그 후엔 오른쪽 자식 노드 역시 NULL이 아닐 때 방문한다. 방문 처리는 순환을 사용한다. 부모 노드를 처리한 후 자식 노드를 처리할 때, 예시로 모든 노드의 레벨을 계산할 때 이를 사용한다. 루트 노드의 레벨이 1이고 어떤 노드의 레벨은 부모 노드의 레벨보다 1이 크기 때문이다.
중위 순회는 왼쪽 서브트리 - 루트 노드 - 오른쪽 서브트리 순으로 방문한다.
void inorder(BinaryNode *node) {
if( node != NULL ) {
if( node->getLeft() != NULL ) inorder(node->getLeft());
printf( " [%c] ", node->getData());
if( node->getRight()!= NULL ) inorder(node->getRight());
}
}BinaryNode의 node 포인터를 매개 변수로 하여 node가 NULL이 아닐 때 if문을 처리한다. node의 왼쪽 자식 노드가 NULL이 아니면 방문하고 루트 노드를 출력한 다음 오른쪽 자식 노드도 NULL이 아닐 때 방문한다. 자식 노드를 방문하는 것은 모두 순회 연산으로 처리된다.
후위 순회는 왼쪽 서브트리, 오른쪽 서브트리를 방문한 후 루트 노드를 마지막으로 방문한다.
void postorder(BinaryNode *node) {
if( node != NULL ) {
if( node->getLeft() != NULL ) postorder(node->getLeft());
if( node->getRight()!= NULL ) postorder(node->getRight());
printf( " [%c] ", node->getData());
}
}node 포인터가 NULL이 아닐 때 왼쪽 서브트리부터 방문하며 NULL이 아닌 상태에서 방문이 끝나면 오른쪽 서브 트리로 옮겨간다. 왼쪽, 오른쪽 순서로 노드 방문이 끝나면 루트 노드를 출력한다. 역시 순회 처리로 함수를 구현한다. 자식 노드를 처리한 후 부모 노드를 처리해야 하는 문제, 예를 들어, 디렉터리의 용량을 계산할 때 이를 사용한다. 하위 디렉터리 용량이 계산되어야만 현재 디렉터리의 용량 계산이 가능하기 때문이다.
동일한 트리로 전위, 중위, 후위 순회 방식 별 노드를 방문하는 순서를 나타내면 다음과 같다.
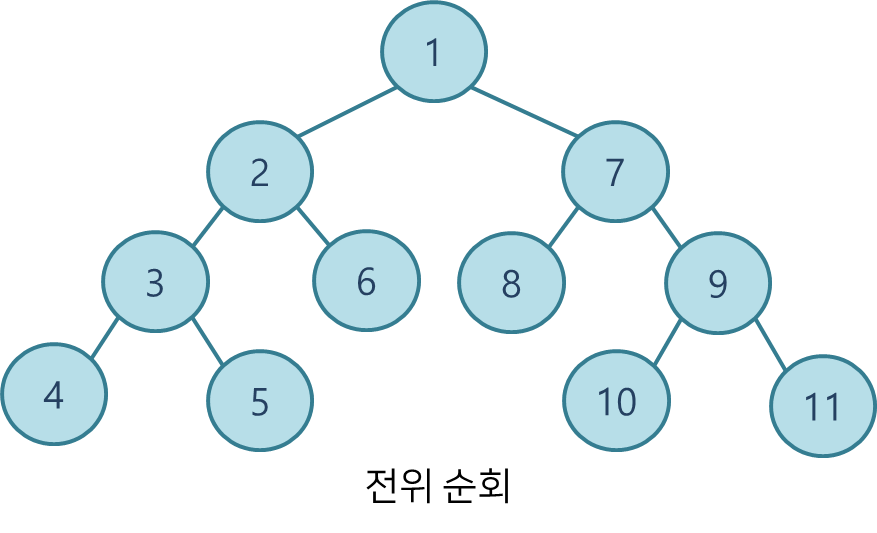

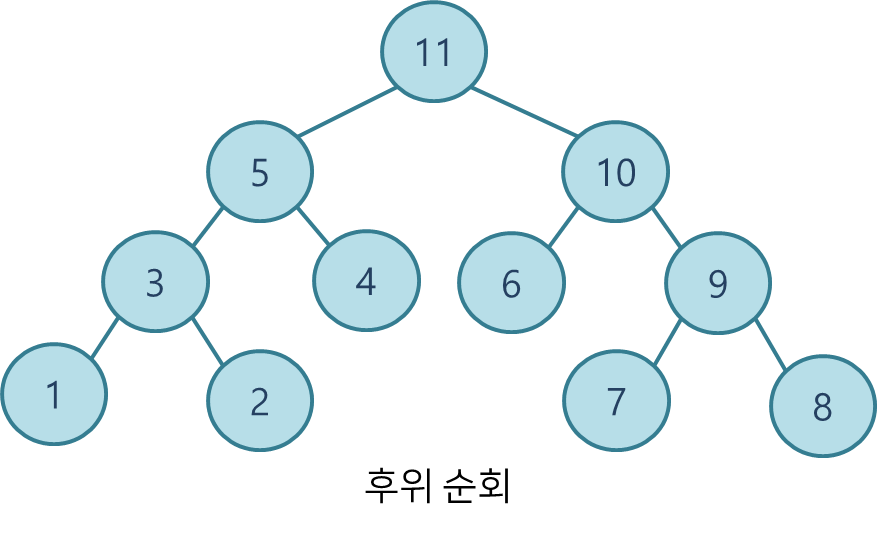
레벨 순회

레벨 순회level order는 각 노드를 레벨 순으로 검사하는 순회 방법으로 표준적인 순회 방법은 아니지만 꽤 많이 사용된다. 루트 노드의 레벨이 1이고 아래로 내려갈수록 레벨은 증가한다. 동일한 레벨에서는 좌에서 우로 방문한다. 앞의 세 가지 표준 순회 방법은 순환을 사용하므로 내부적으로 스택이 사용되었다고 볼 수 있으나 레벨 순회는 큐를 사용한다.
큐에서 노드를 하나 꺼내 방문하고 그 자식들을 큐에 삽입한다. 이때 자식이 없으면 삽입하지 않고 왼쪽 자식을 먼저, 오른쪽 자식을 다음에 처리한다. 이 과정을 큐가 공백 상태가 될 때까지 반복한다. 초기 상태의 큐는 루트 노드만 가진다.
그림 8.9를 예로 설명하자면 먼저 루트 노드인 +가 큐에 입력된 상태에서 순회가 시작된다. 큐에서 하나를 삭제하면 +가 나오고 노드 +의 왼쪽 자식 *과 /를 큐에 삽입한다. 또 큐에서 한 노드(*)를 꺼내고 같은 과족을 반복한다. 표준적인 순회 방법과 다르게 순환을 사용하지 않음에 유의해야 한다. 따라서 별도의 함수 구현이 필요 없고 노드 클래스가 아닌 트리 클래스에서 구현되어야 한다.
void levelorder( ) {
printf("\nlevelorder: ");
if( !isEmpty() ) {
CircularQueue q;
q.enqueue( root );
while ( !q.isEmpty() ) {
BinaryNode* n = q.dequeue();
if( n != NULL ) {
printf(" [%c] ", n->getData());
q.enqueue(n->getLeft ());
q.enqueue(n->getRight());
}
}
}
printf("\n");
}공백 트리가 아닌 경우만 처리하게 if문을 앞에 두고, 원형 큐 객체를 생성한다. 해당 큐 객체에 루트 노드를 삽입한 후, 큐가 공백 상태가 아닌 동안 큐의 맨 앞 노드 n을 꺼내고 먼저 노드의 정보를 출력한다. n의 왼쪽 자식 노드를 큐에 삽입한 후 n의 오른쪽 자식 노드를 큐에 삽입한다.
8.6 이진트리 연산
순회 이외의 이진트리와 관련된 여러 가지 연산들을 살펴보자.
트리의 노드 개수 구하기
기본적으로 트리의 노드 개수를 세기 위해서는 트리의 모든 노드들을 순회하여야 한다. 트리의 노드 개수는 왼쪽 서브트리의 노드 개수와 오른쪽 서브트리의 노드 개수에 루트 노드를 더하면 된다. 이는 순환 호출로 계산한다.
//트리의 노드 개수를 구하는 함수
int getCount() { return isEmpty() ? 0 : getCount(root); }
//순환 호출에 의해 node를 루트로 하는 서브트리의 노드 수 개수 함수
int getCount(BinaryNode *node) {
if( node == NULL ) return 0;
return 1 + getCount(node->getLeft()) + getCount(node->getRight());
}
첫 번째 getCount()는 외부 인터페이스를 위한 함수이고 공백 트리이면 0을 반환하고 아니면 getCount(root)를 호출하여 결과를 반환한다. 두 번째 함수는 순환을 이용하여 현재 노드 node를 루트로 하는 서브트리의 노드 수를 계산한다. node가 NULL이면 공백 트리이므로 0으로 반환하고 공백 트리가 아니면 왼쪽 서브트리의 노드 개수와 오른쪽 서브트리의 노드 개수를 합하고 현재 노드인 1을 더한 값을 반환한다.
단말 노드 개수 구하기
단말 노드의 개수를 세려면 역시 트리 내 모든 노드들을 순회하여야 한다. 순회 중 만약 왼쪽 자식과 오른쪽 자식이 동시에 0이 되면 단말 노드이므로 1을 반환하고 그렇지 않으면 비단말 노드이므로 각각의 서브트리에 대하여 순환 호출한 다음 반환되는 값을 서로 더한다.
//트리의 단말노드 개수를 구하는 함수
int getLeafCount(){ return isEmpty() ? 0 : getLeafCount(root); }
//순환 호출에 의해 node를 루트로 하는 서브트리의 단말 노드 수 계산 함수
int getLeafCount(BinaryNode *node) {
if( node == NULL ) return 0;
if( node->isLeaf() ) return 1;
else return getLeafCount(node->getLeft()) + getLeafCount(node->getRight());
}getLeafCount() 함수는 외부 인터페이스를 위한 함수. 공백 트리이면 0을 반환하고 아니면 getLeafCount(root)을 호출하여 결과를 반환한다. 두 번째 함수는 순환을 이용하여 현재 노드 node를 루트로 하는 서브트리의 단말 노드 수를 계산하는 함수다. node가 NULL이면 공백 트리이므로 0을 반환하고 node 가 단말 노드이면 1을 반환한다. 단말 노드가 아니면 왼쪽 서브트리의 단말노드 개수와 오른쪽 서브트리의 단말 노드 개수를 합한 값을 반환한다.
높이 구하기
트리의 높이를 구할 때에도 먼저 각 서브트리에 대하여 순환 호출을 하여야 한다. 순환 호출이 끝나면 각각 서브트리로부터 서브트리의 높이가 반환되어 왔을 것이다. 그 후 왼쪽 서브트리와 오른쪽 서브트리 중에서 더 높은 트리를 먼저 찾는다. 현재 트리의 높이는 더 높은 서브트리의 높이보다 1 높다. 높이를 구할 땐 반환 값을 서로 더하지 않는다.
//트리의 높이를 구하는 함수
int getHeight() { return isEmpty() ? 0 : getHeight(root); }
//순환 호출에 의해 node를 루트로 하는 서브트리의 높이 계산 함수
int getHeight(BinaryNode *node) {
if( node == NULL ) return 0;
int hLeft = getHeight(node->getLeft());
int hRight = getHeight(node->getRight());
return (hLeft>hRight) ? hLeft+1 : hRight+1;
}첫 번째 함수는 외부 인터페이스를 위한 함수로 공백 트리이면 0을 반환하고 아니면 getHeight(root)를 호출하여 결과를 반환한다. 두 번째 함수는 순환을 이용하여 트리의 높이를 계산하는데 node가 NULL이면 공백 트리이므로 0을 반환하고 그렇지 않으면 왼쪽 서브트리의 높이를 계산하여 hLeft에 저장하고 오른쪽 서브트리의 높이를 계산하여 hRight에 저장한다. hLeft와 hRight 중 큰 값을 선택하고 1을 더해 값을 반환한다.
8.7 이진트리 응용
수식 트리
이진트리 순회는 수식 트리expression tree를 처리하는 데 사용될 수 있다. 수식 트리는 산술식이나 논리식의 연산자와 피연산자들로 구성되는데 피연산자는 단말 노드, 연산자는 비단말 노드가 된다. 수식 트리에서 각 이진 연산자에 대하여, 왼쪽 서브트리는 왼쪽 피연산자, 오른쪽 서브트리는 오른쪽 피연산자를 나타낸다.

이들 수식 트리를 전위, 중위, 후위의 순회 방법으로 읽으면 각각 전위 표기 수식, 중위 표기 수식, 후위 표기 수식이 된다.
| 수식 | a + b | a - (b x c) | (a < b) or (c < d) |
| 전위 순회 | + a b | - a X b c | or < a b < c d |
| 중위 순회 | a + b | a - b X c | a < b or c < d |
| 후위 순회 | a b + | a b c X - | a b < c d < or |
수식 트리의 루트 노드는 연산자이고 따라서 이 연산자의 피연산자인 서브트리들만 계산되면 전체 수식을 계산할 수 있다. 각각의 서브트리도 마찬가지로 자식 노드만 계산되면 루트에 저장된 연산자를 이용하여 수식 계산이 가능하다. 따라서 후위 순회를 사용하여야 한다.
//수식 트리 계산 함수
int evaluate() { return evaluate(root); }
// 순환 호출에 의해 node를 루트로 하는 수식 트리의 계산 함수
int evaluate(BinaryNode *node) {
if( node == NULL ) return 0;
if( node->isLeaf() ) return node->getData();
else {
int op1 = evaluate(node->getLeft());
int op2 = evaluate(node->getRight());
switch(node->getData()){
case '+': return op1+op2;
case '-': return op1-op2;
case '*': return op1*op2;
case '/': return op1/op2;
}
return 0;
}
}첫 번째 함수는 외부 인터페이스를 위한 함수로 evaluate(root)를 호출하여 반환한다. 두 번째 함수는 순환을 이요하여 수식 트리를 계산하는데 node가 NULL이면 공백 트리이므로 0을 반환한다. 또 단말 노드이면 피연산자이므로 그 노드의 값을 반환한다. 단말 노드가 아니면, 왼쪽 서브트리를 계산하여 결과를 op1에 저장한 후 오른쪽 서브트리의 결과는 op2에 저장한다. 이때 순환 호출을 사용한다. 현재 노드(연산자)의 연산자를 검사하여 +, - *, /인 경우 그에 따른 연산을 처리하여 결과를 반환한다.
디렉터리 용량 계산
이진트리 순회는 디렉터리 용량 계산에도 쓰이나, 이진트리를 사용하므로 하나의 디렉터리 안에 다른 디렉터리가 2개를 초과하지 않아야 한다. 용량 계산은, 한 디렉터리 안에 다른 디렉터리가 존재할 수 있으니 먼저 서브 디렉토리의 용량을 모두 계산한 다음 루트 디렉터리를 계산하여야 한다. 따라서 후위 순회를 사용하되, 순환 호출되는 순회 함수가 용량을 반환하여야 한다.
//디렉터리 용량 계산 함수
int calcSize() { return calcSize(root); }
//순환 호출에 의해 node를 루트로 하는 트리의 전체 용량 계산 함수
int calcSize(BinaryNode *node) {
if( node == NULL ) return 0;
return node->getData() + calcSize(node->getLeft()) + calcSize(node->getRight());
}첫 번째 함수는 외부 인터페이스를 위한 함수로 calcSize(root)를 호출하여 결과를 반환하고 두 번째 함수는 순환을 이용하여 디렉터리 용량을 계산하는 함수이다. node가 NULL이면 공백 트리이므로 0을 반환하고 그렇지 않으면 왼쪽 서브트리와 오른쪽 서브트리의 용량을 각각 구해 더하고 현재 디렉터리의 용량을 더한 값을 반환한다.
8.8 스레드 이진트리
이진트리의 3가지 표준 순회는 순환 호출을 사용(내부적인 스택도 사용)하고 레벨 순회는 큐를 사용한다. 순환 호출이나 추가적인 자료구조 없이 순회를 구현할 순 없을까?
이진트리의 노드엔 많은 NULL 링크들이 존재한다. 만약 노드가 n개이면 각 노드 당 2개의 링크가 존재하므로 전체 링크의 수는 2n 개다. 이들 중 루트를 제외한 n-1개의 노드가 부모와 연결되어 있으므로 2n개 중 n-1개를 제외한 n+1개의 링크가 항상 NULL이다. 이들을 잘 활용하여 순환 호출 없이 순회할 수 있지 않을까? 이러한 아이디어를 구현한 트리를 스레드 이진트리threaded binary tree이다.
스레드 이진트리
중위 순회를 위한 스레드 이진트리를 보자. 트리의 노드들을 중위 순회로 방문할 때 어떤 노드 바로 앞에 방문되는 노드를 중위 선행자inorder predecessor라고 하고, 바로 다음에 방문하는 노드를 중위 후속자inorder successor라고 한다. 스레드 이진트리에서는 NULL 링크를 재사용하는데, 링크 값이 NULL을 갖는 대신에 중위 선행자나 중위 후속자를 저장시켜 놓는 것이다.
그림 8.11의 파란색 화살표는 해당 노드의 중위 후속자를, 빨간색 화살표는 중위 선행자를 가리킨다.

이런 식으로 NULL 링크에 스레드가 저장되면 링크에 자식을 가리키는 포인터가 저장되어 있는지, NULL이 저장되어야 하는데 그 자리를 스레드로 대신 저장되어 있는지를 구별하는 필드(bool 변수)가 필요하다.
스레드 이진트리의 구현
BinaryNode.h를 스레드 이진트리를 구현하기 위해 변형하는데, 먼저 링크의 구별을 위해 데이터 멤버에 bThread를 추가하여 오른쪽 링크가 스레드이면 true로, 아니면 false로 한다. 이 멤버 추가에 따라 노드 클래스의 생성자도 수정하여야 한다. 결국 bThread가 true이면 right는 중위 후속자이고 flase이면 오른쪽을 자식을 가리키는 포인터인 것이다.
#pragma once
#include <stdio.h>
class ThreadedBinNode
{
protected:
int data;
ThreadedBinNode *left;
ThreadedBinNode *right;
public:
bool bThread;
ThreadedBinNode( int val=0, ThreadedBinNode *l=NULL, ThreadedBinNode *r=NULL, bool bTh=false)
: data(val), left(l), right(r), bThread(bTh) { }
int getData () { return data; }
void setRight(ThreadedBinNode *r) { right= r; }
ThreadedBinNode* getLeft () { return left; }
ThreadedBinNode* getRight() { return right; }
};
스레드 이진트리를 위한 노드 클래스로, 데이터 멤버 변수에는 데이터 필드를 가리키는 int형 data 변수, 왼쪽 자식 노드와 오른쪽 자식 노드를 각각 가리키는 포인터 변수인 left, right를 선언한다. 또 링크의 구별을 위해 bool 타입의 bThread를 선언하여 오른쪽 링크가 스레드이면 true로, 아니면 false로 유지한다. true이면 right는 중위 후속자이고 false를 리턴하면 오른쪽 자식 노드를 가리키는 포인터이다. 생성자는 디폴트 매개변수로 멤버 초기화 리스트를 이용해서 초기화하고 새로 추가한 bThread에 대한 생성자도 추가한다. getData()는 해당 노드의 데이터를 반환하고 setRight()는 매개변수로 받은 포인터 변수 r을 right에 저장한다. getLeft()와 getRight()는 각각 왼쪽과 오른쪽 자식 노드를 반환한다.
또 노드 p의 중위 후속자를 반환하는 findSuccessor()를 통해 p의 bThread가 ture이면 오른쪽 자식이 중위 후속자이므로 오른쪽 자식을 반환하고 NULL이면 더 이상 후속자가 없다는 뜻이므로 NULL을 반환한다. bThread가 false면 서브트리의 가장 왼쪽 노드로 왼쪽 링크를 타고 NULL이 될 때까지 이동한 후 최종적인 왼쪽 자식 노드의 포인터를 반환한다.
#pragma once
#include "ThreadedBinNode.h"
class ThreadedBinTree
{
ThreadedBinNode* root;
public:
ThreadedBinTree(): root(NULL) { }
~ThreadedBinTree() { }
void setRoot(ThreadedBinNode* node) { root = node; }
ThreadedBinNode* getRoot() { return root; }
bool isEmpty() { return root==NULL; }
//스레드 방식의 전위 순회 함수
void threadedInorder() {
if( !isEmpty() ) {
printf("스레드 이진 트리: ");
ThreadedBinNode *q = root;
while (q->getLeft()) q = q->getLeft();
do {
printf("%c ", q->getData());
q = findSuccessor(q);
} while(q);
printf("\n");
}
}
//후속자 함수 호출
ThreadedBinNode* findSuccessor(ThreadedBinNode* p){
ThreadedBinNode *q = p->getRight();
if( q==NULL || p->bThread ) return q;
while( q->getLeft() != NULL ) q = q->getLeft();
return q;
}
};
ThreadedBinTree는 스레드 이진트리를 위한 클래스로 ThreadedBinTree의 포인터형 변수 root를 먼저 선언하고, NULL로 생성자에서 초기화한다. setRoot()함수는 해당 노드를 루트 노드로 설정하고 isEmpty()함수는 bool타입으로, root가 NULL일 때 true를 반환한다. threadedInorder() 함수는 스레드 방식의 전위 순회 함수를 구현한 것으로 트리가 공백 상태가 아닐 때 처리를 진행한다. 먼저 while문을 통해 노드 q의 링크를 타고 가장 왼쪽의 노드로 이동한 후 그 데이터를 출력하고 다음 노드를 찾아 q를 갱신한다. 그 후에는 순환 호출을 사용하는 것이 아니라 후속자 함수 findSuccessor()을 호출하여 후속자를 찾는다. 해당 노드의 오른쪽 자식 포인터를 가지고, 그 포인터가 NULL이거나, 스레드이면 오른쪽 포인터를 반환한다. 오른쪽 자식 노드라면 다시 가장 왼쪽 노드로 이동하여 반환한다.
스레드 트리는 순회를 빠르게 하는 장점이 있으나 스레드 설정 때문에 삽입이나 삭제 함수가 더욱 복잡하다.
'ETC. > Data Structure' 카테고리의 다른 글
| 10 우선순위 큐 (0) | 2019.12.04 |
|---|---|
| 09 이진 탐색 트리 (0) | 2019.12.04 |